%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
import casadi
u = casadi.SX.sym('u')
def get_circle_pnt(u, pos, radius, offset=0.0):
x = pos[0] + radius * np.cos(2 * np.pi * u + offset)
y = pos[1] + radius * np.sin(2 * np.pi * u + offset)
return x, y
def get_circle(pos, radius, offset=0.0):
u = np.linspace(0, 1, 50)
return get_circle_pnt(u, pos, radius, offset)
def get_frame(angle):
return np.array([[np.cos(angle), -np.sin(angle)],[np.sin(angle), np.cos(angle)]])
radius = 5
wp_1 = np.array([2, 3])
heading_1 = 10 * np.pi / 180
wp_2 = np.array([20, 32])
heading_2 = 130 * np.pi / 180
frame_1 = get_frame(heading_1)
frame_2 = get_frame(heading_2)
center_1 = dict(R=wp_1 - radius * frame_1[:, 1].flatten(),
L=wp_1 + radius * frame_1[:, 1].flatten())
center_2 = dict(R=wp_2 - radius * frame_2[:, 1].flatten(),
L=wp_2 + radius * frame_2[:, 1].flatten())
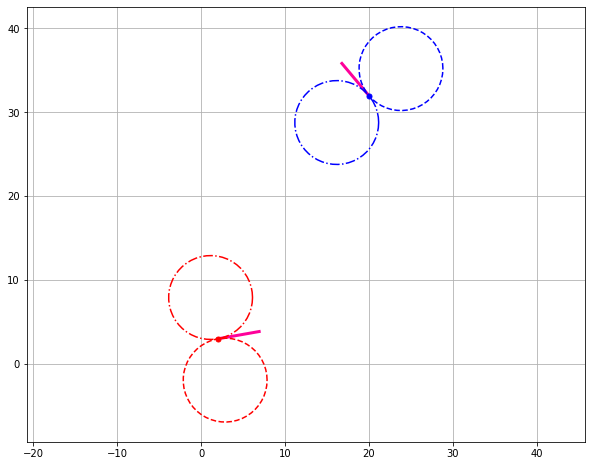
def plot_base():
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
# Plot first waypoint's L and R circles
ax.plot([wp_1[0], wp_1[0] + 5 * np.cos(heading_1)], [wp_1[1], wp_1[1] + 5 * np.sin(heading_1)], color='xkcd:neon pink', linewidth=3)
ax.plot([wp_1[0]], [wp_1[1]], '.r', markersize=10)
x, y = get_circle(center_1['L'], radius)
ax.plot(x, y, '-.r')
x, y = get_circle(center_1['R'], radius)
ax.plot(x, y, '--r')
# Plot second waypoint's L and R circles
x, y = get_circle(wp_2, radius)
ax.plot([wp_2[0], wp_2[0] + 5 * np.cos(heading_2)], [wp_2[1], wp_2[1] + 5 * np.sin(heading_2)], color='xkcd:neon pink', linewidth=3)
ax.plot([wp_2[0]], [wp_2[1]], '.b', markersize=10)
x, y = get_circle(center_2['L'], radius)
ax.plot(x, y, '-.b')
x, y = get_circle(center_2['R'], radius)
ax.plot(x, y, '--b')
ax.axis('equal')
ax.grid(True)
return ax
plot_base()
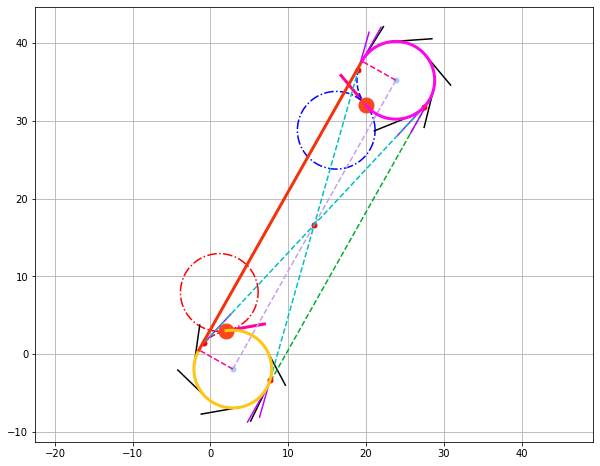
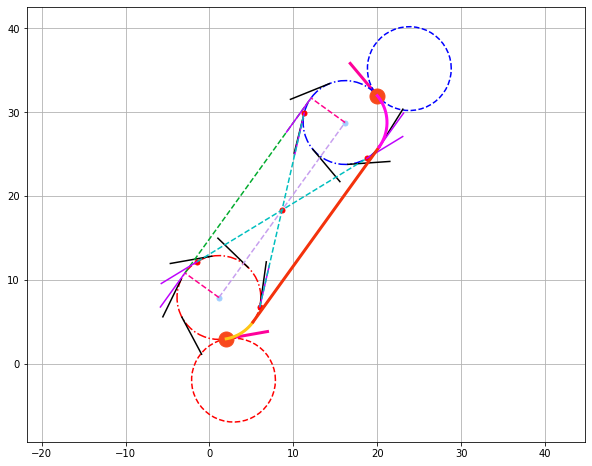
print('RSR')
u1 = casadi.SX.sym('u1')
u2 = casadi.SX.sym('u2')
def get_tangents(center_1, radius_1, heading_1, delta_1, center_2, radius_2, heading_2, delta_2):
output = dict()
phi_1 = 2 * np.pi * u1 * delta_1 + heading_1 - delta_1 * np.pi / 2
phi_2 = 2 * np.pi * u2 * delta_2 + heading_2 - delta_2 * np.pi / 2
u1_func = lambda angle: (angle - heading_1 + delta_1 * np.pi / 2) / (delta_1 * 2 * np.pi)
u2_func = lambda angle: (angle - heading_2 + delta_2 * np.pi / 2) / (delta_2 * 2 * np.pi)
# Make tangents vector functions
tan_1 = casadi.cross(np.array([0, 0, 1]),
np.array([delta_1 * radius * np.cos(phi_1), delta_1 * radius * np.sin(phi_1), 0]))[0:2]
tan_2 = casadi.cross(np.array([0, 0, 1]),
np.array([delta_2 * radius * np.cos(phi_2), delta_2 * radius * np.sin(phi_2), 0]))[0:2]
# Make circle functions
circle_1_func = center_1 + radius_1 * np.array([np.cos(phi_1), np.sin(phi_1)])
circle_2_func = center_2 + radius_2 * np.array([np.cos(phi_2), np.sin(phi_2)])
# Plot the circles
ax = plot_base()
## Plot the circle center points
ax.plot([center_1[0]], [center_1[1]], marker='.', color='xkcd:baby blue', markersize=10)
ax.plot([center_2[0]], [center_2[1]], marker='.', color='xkcd:baby blue', markersize=10)
## Plot a couple of tangent vectors
for i in np.linspace(0.2, 0.8, 5):
c1 = casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [i])
t1 = casadi.substitute(tan_1, casadi.vertcat(*[u1]), [i])
t1 *= 5 / casadi.norm_2(t1)
ax.plot([c1[0], c1[0] + t1[0]],
[c1[1], c1[1] + t1[1]], 'k')
c2 = casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [i])
t2 = casadi.substitute(tan_2, casadi.vertcat(*[u2]), [i])
t2 *= 5 / casadi.norm_2(t2)
ax.plot([c2[0], c2[0] + t2[0]],
[c2[1], c2[1] + t2[1]], 'k')
## Plot line connecting the circle centers
ax.plot([center_1[0], center_2[0]], [center_1[1], center_2[1]], linestyle='--', color='xkcd:lavender')
## Plot the starting point of each circle
c1 = casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [0])
c2 = casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [0])
ax.plot([c1[0]], [c1[1]], marker='o', color='xkcd:reddish orange', markersize=15)
ax.plot([c2[0]], [c2[1]], marker='o', color='xkcd:reddish orange', markersize=15)
# Compute the line connecting the circle's centers
d = center_2 - center_1
# Calculate normal vector to the connecting line
n = np.dot(get_frame(np.pi / 2), d / np.linalg.norm(d))
## Plotting the normal vectors
ax.plot([center_1[0], center_1[0] + radius_1 * n[0]], [center_1[1], center_1[1] + radius_1 * n[1]], linestyle='--', color='xkcd:hot pink')
ax.plot([center_2[0], center_2[0] + radius_2 * n[0]], [center_2[1], center_2[1] + radius_2 * n[1]], linestyle='--', color='xkcd:hot pink')
##########################################################
# Compute the first tangent
## Compute the normal vector's angle
n_angle = np.arctan2(n[1], n[0])
## Compute the parameter for the tangent points on both circles
u1_opt = u1_func(n_angle)
if u1_opt < 0:
u1_opt = u1_opt + 1
u2_opt = u2_func(n_angle)
if u2_opt < 0:
u2_opt = u2_opt + 1
## Compute the points on the circles for the first tangent
c1 = casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [u1_opt])
c2 = casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [u2_opt])
tangent_1 = c2 - c1
tangent_1 /= casadi.norm_2(tangent_1)
ax.plot([c1[0], c2[0]], [c1[1], c2[1]], linestyle='--', color='xkcd:kelly green')
## Compute the tangent vectors on the circles
t1 = casadi.substitute(tan_1, casadi.vertcat(*[u1]), [u1_opt])
t1 /= casadi.norm_2(t1)
t2 = casadi.substitute(tan_2, casadi.vertcat(*[u2]), [u2_opt])
t2 /= casadi.norm_2(t2)
diff = float(casadi.norm_2(tangent_1 - t1) + casadi.norm_2(tangent_1 - t2))
if np.isclose(diff, 0):
u = np.arange(0, u1_opt, 0.001)
output['C1'] = [casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [ui]) for ui in u]
output['S'] = [casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [u1_opt]), casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [u2_opt])]
u = np.arange(u2_opt, 1, 0.001)
output['C2'] = [casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [ui]) for ui in u]
## Plot the tangent vectors on the circles that are parallel to the first tangent
ax.plot([c1[0], c1[0] + radius_1 * t1[0]], [c1[1], c1[1] + radius_1 * t1[1]], linestyle='-', color='xkcd:bright purple')
ax.plot([c2[0], c2[0] + radius_2 * t2[0]], [c2[1], c2[1] + radius_2 * t2[1]], linestyle='-', color='xkcd:bright purple')
##########################################################
# Compute the second tangent
n_angle = np.arctan2(-n[1], -n[0])
u1_opt = u1_func(n_angle)
if u1_opt < 0:
u1_opt = u1_opt + 1
u2_opt = u2_func(n_angle)
if u2_opt < 0:
u2_opt = u2_opt + 1
c1 = casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [u1_opt])
c2 = casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [u2_opt])
tangent_2 = c2 - c1
tangent_2 /= casadi.norm_2(tangent_2)
## Plotting the second tangent
ax.plot([c1[0], c2[0]], [c1[1], c2[1]], linestyle='--', color='xkcd:kelly green')
## Compute the tangent vectors on the circles
t1 = casadi.substitute(tan_1, casadi.vertcat(*[u1]), [u1_opt])
t1 /= casadi.norm_2(t1)
t2 = casadi.substitute(tan_2, casadi.vertcat(*[u2]), [u2_opt])
t2 /= casadi.norm_2(t2)
diff = float(casadi.norm_2(tangent_2 - t1) + casadi.norm_2(tangent_2 - t2))
if np.isclose(diff, 0):
u = np.arange(0, u1_opt, 0.001)
output['C1'] = [casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [ui]) for ui in u]
output['S'] = [casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [u1_opt]), casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [u2_opt])]
u = np.arange(u2_opt, 1, 0.001)
output['C2'] = [casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [ui]) for ui in u]
## Plot the tangent vectors on the circles that are parallel to the second tangent
ax.plot([c1[0], c1[0] + radius_1 * t1[0]], [c1[1], c1[1] + radius_1 * t1[1]], linestyle='-', color='xkcd:bright purple')
ax.plot([c2[0], c2[0] + radius_2 * t2[0]], [c2[1], c2[1] + radius_2 * t2[1]], linestyle='-', color='xkcd:bright purple')
##########################################################
# Computing inner tangents
# Calculate the intersection point of the two tangent lines
xp = (center_1[0] * radius_1 + center_2[0] * radius_2) / (radius_1 + radius_2)
yp = (center_1[1] * radius_1 + center_2[1] * radius_2) / (radius_1 + radius_2)
ax.plot([xp], [yp], '.r', markersize=10)
# Third and fourth tangents
xt1 = (radius_1**2 * (xp - center_1[0]) + radius_1 * (yp - center_1[1]) * np.sqrt((xp - center_1[0])**2 + (yp - center_1[1])**2 - radius_1**2)) / ((xp - center_1[0])**2 + (yp - center_1[1])**2) + center_1[0]
xt2 = (radius_1**2 * (xp - center_1[0]) - radius_1 * (yp - center_1[1]) * np.sqrt((xp - center_1[0])**2 + (yp - center_1[1])**2 - radius_1**2)) / ((xp - center_1[0])**2 + (yp - center_1[1])**2) + center_1[0]
yt1 = ((radius_1**2 * (yp - center_1[1])) - radius_1 * (xp - center_1[0]) * np.sqrt((xp - center_1[0])**2 + (yp - center_1[1])**2 - radius_1**2)) / ((xp - center_1[0])**2 + (yp - center_1[1])**2) + center_1[1]
yt2 = ((radius_1**2 * (yp - center_1[1])) + radius_1 * (xp - center_1[0]) * np.sqrt((xp - center_1[0])**2 + (yp - center_1[1])**2 - radius_1**2)) / ((xp - center_1[0])**2 + (yp - center_1[1])**2) + center_1[1]
## Plotting the tangent points on the first circle
ax.plot([xt1, xt2], [yt1, yt2], '.r', markersize=10)
xt3 = (radius_2**2 * (xp - center_2[0]) + radius_2 * (yp - center_2[1]) * np.sqrt((xp - center_2[0])**2 + (yp - center_2[1])**2 - radius_2**2)) / ((xp - center_2[0])**2 + (yp - center_2[1])**2) + center_2[0]
xt4 = (radius_2**2 * (xp - center_2[0]) - radius_2 * (yp - center_2[1]) * np.sqrt((xp - center_2[0])**2 + (yp - center_2[1])**2 - radius_2**2)) / ((xp - center_2[0])**2 + (yp - center_2[1])**2) + center_2[0]
yt3 = ((radius_2**2 * (yp - center_2[1])) - radius_2 * (xp - center_2[0]) * np.sqrt((xp - center_2[0])**2 + (yp - center_2[1])**2 - radius_2**2)) / ((xp - center_2[0])**2 + (yp - center_2[1])**2) + center_2[1]
yt4 = ((radius_2**2 * (yp - center_2[1])) + radius_2 * (xp - center_2[0]) * np.sqrt((xp - center_2[0])**2 + (yp - center_2[1])**2 - radius_2**2)) / ((xp - center_2[0])**2 + (yp - center_2[1])**2) + center_2[1]
## Plotting the tangent points on the second circle
ax.plot([xt3, xt4], [yt3, yt4], '.r', markersize=10)
# Third tangent
u1_opt = u1_func(np.arctan2(yt1 - center_1[1], xt1 - center_1[0]))
if u1_opt < 0:
u1_opt = u1_opt + 1
u2_opt = u2_func(np.arctan2(yt3 - center_2[1], xt3 - center_2[0]))
if u2_opt < 0:
u2_opt = u2_opt + 1
c1 = casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [u1_opt])
c2 = casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [u2_opt])
t1 = casadi.substitute(tan_1, casadi.vertcat(*[u1]), [u1_opt])
t1 /= casadi.norm_2(t1)
t2 = casadi.substitute(tan_2, casadi.vertcat(*[u2]), [u2_opt])
t2 /= casadi.norm_2(t2)
## Plot the tangent vectors on the circles that are parallel to the third tangent
ax.plot([c1[0], c1[0] + radius_1 * t1[0]], [c1[1], c1[1] + radius_1 * t1[1]], linestyle='-', color='xkcd:bright purple')
ax.plot([c2[0], c2[0] + radius_2 * t2[0]], [c2[1], c2[1] + radius_2 * t2[1]], linestyle='-', color='xkcd:bright purple')
tangent_3 = np.array([xt3 - xt1, yt3 - yt1])
tangent_3 /= np.linalg.norm(tangent_3)
diff = float(casadi.norm_2(tangent_3 - t1) + casadi.norm_2(tangent_3 - t2))
if np.isclose(diff, 0):
u = np.arange(0, u1_opt, 0.001)
output['C1'] = [casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [ui]) for ui in u]
output['S'] = [casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [u1_opt]), casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [u2_opt])]
u = np.arange(u2_opt, 1, 0.001)
output['C2'] = [casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [ui]) for ui in u]
# Fourth tangent
u1_opt = u1_func(np.arctan2(yt2 - center_1[1], xt2 - center_1[0]))
if u1_opt < 0:
u1_opt = u1_opt + 1
u2_opt = u2_func(np.arctan2(yt4 - center_2[1], xt4 - center_2[0]))
if u2_opt < 0:
u2_opt = u2_opt + 1
c1 = casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [u1_opt])
c2 = casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [u2_opt])
t1 = casadi.substitute(tan_1, casadi.vertcat(*[u1]), [u1_opt])
t1 /= casadi.norm_2(t1)
t2 = casadi.substitute(tan_2, casadi.vertcat(*[u2]), [u2_opt])
t2 /= casadi.norm_2(t2)
## Plot the tangent vectors on the circles that are parallel to the fourth tangent
ax.plot([c1[0], c1[0] + radius_1 * t1[0]], [c1[1], c1[1] + radius_1 * t1[1]], linestyle='-', color='xkcd:bright purple')
ax.plot([c2[0], c2[0] + radius_2 * t2[0]], [c2[1], c2[1] + radius_2 * t2[1]], linestyle='-', color='xkcd:bright purple')
tangent_4 = np.array([xt4 - xt2, yt4 - yt2])
tangent_4 /= np.linalg.norm(tangent_4)
diff = float(casadi.norm_2(tangent_4 - t1) + casadi.norm_2(tangent_4 - t2))
if np.isclose(diff, 0):
u = np.arange(0, u1_opt, 0.001)
output['C1'] = [casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [ui]) for ui in u]
output['S'] = [casadi.substitute(circle_1_func, casadi.vertcat(*[u1]), [u1_opt]), casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [u2_opt])]
u = np.arange(u2_opt, 1, 0.001)
output['C2'] = [casadi.substitute(circle_2_func, casadi.vertcat(*[u2]), [ui]) for ui in u]
ax.plot([xt1, xt3], [yt1, yt3], '--c')
ax.plot([xt2, xt4], [yt2, yt4], '--c')
#########################################################
# Plot the path
ax.plot([x[0] for x in output['C1']], [x[1] for x in output['C1']], color='xkcd:golden yellow', linewidth=3)
ax.plot([x[0] for x in output['S']], [x[1] for x in output['S']], color='xkcd:vermillion', linewidth=3)
ax.plot([x[0] for x in output['C2']], [x[1] for x in output['C2']], color='xkcd:bright magenta', linewidth=3)
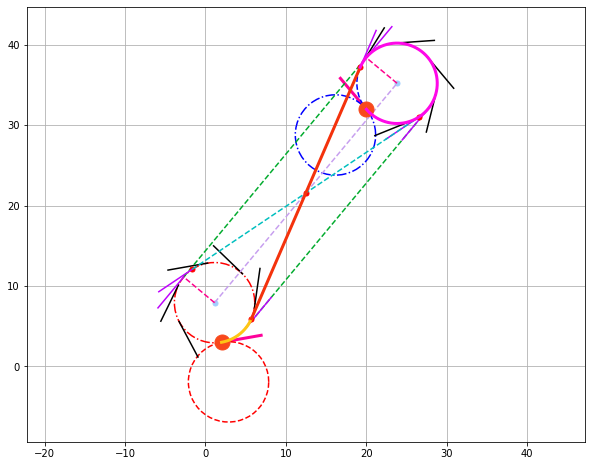
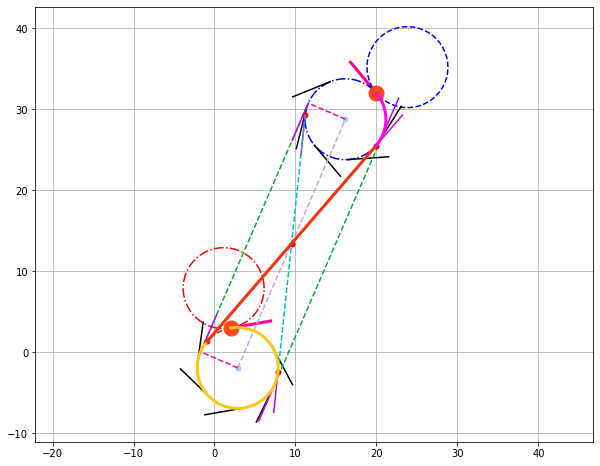
get_tangents(center_1['R'], radius, heading_1, -1, center_2['R'], radius, heading_2, -1)